Manuscrito

Simulación de las caminatas

In [1]:

from numpy.random import randint
from numpy import argmax, arange
from matplotlib.pyplot import plot, hist, scatter

Si tenemos una variable aleatoria \(X \in \{-1,1\}\) con una distribución uniforme. Podemos simularla con:

In [2]:

n_pasos = 100
n_caminatas = 1 

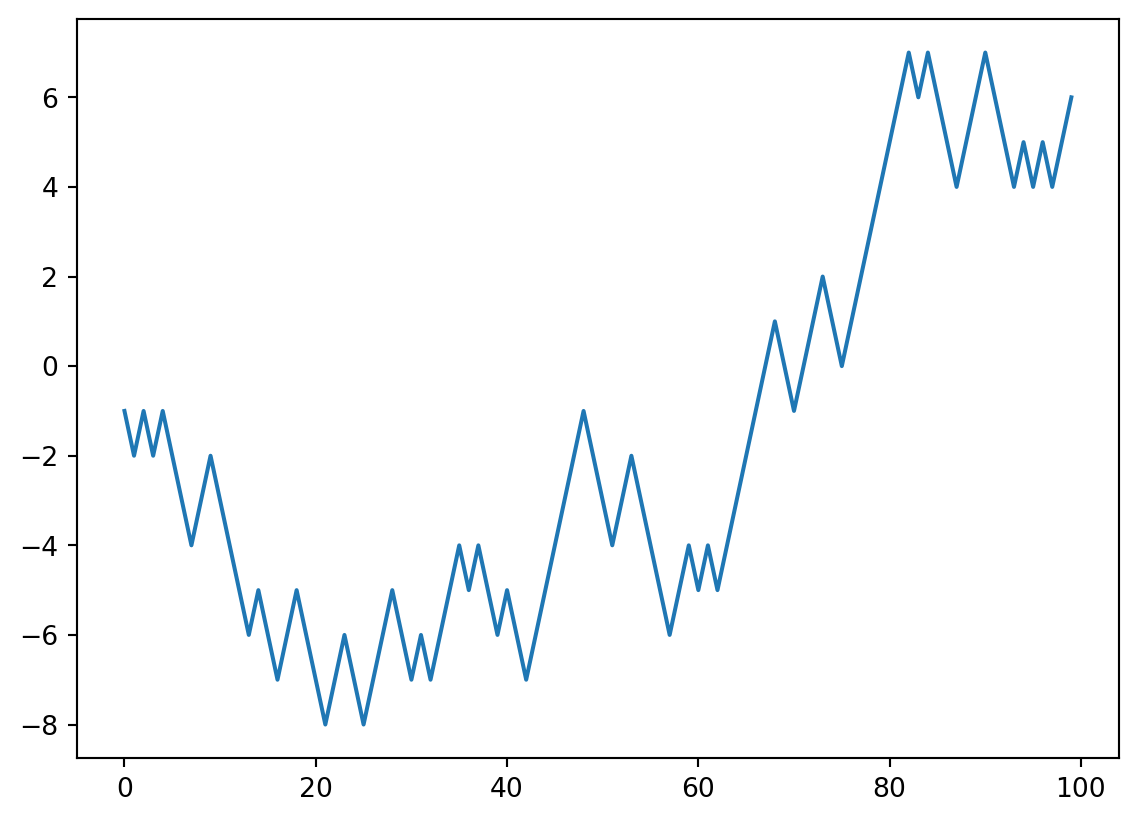
pasos = 2*randint(0,2, (n_pasos, n_caminatas)) - 1

Una caminata aleatoria de largo \(N\) se considera como la trayectoria que realiza una variable aleatoria

\[ S = \sum_{i=1}^{N} X_{i} \tag{1}\]

In [3]:

caminatas = pasos.cumsum(axis=0)
plot(caminatas)

Trayectorias que representan caminatas aleatorias

Queremos estudiar cual es la probabilidad \(P\) de que un caminante regrese al origen en \(n\) pasos.

In [4]:

vuelta_al_origen = argmax(caminatas == 0, axis=0)

In [5]:

h = hist(vuelta_al_origen, bins=30)

Estudio del conjunto de caminatas aleatorias

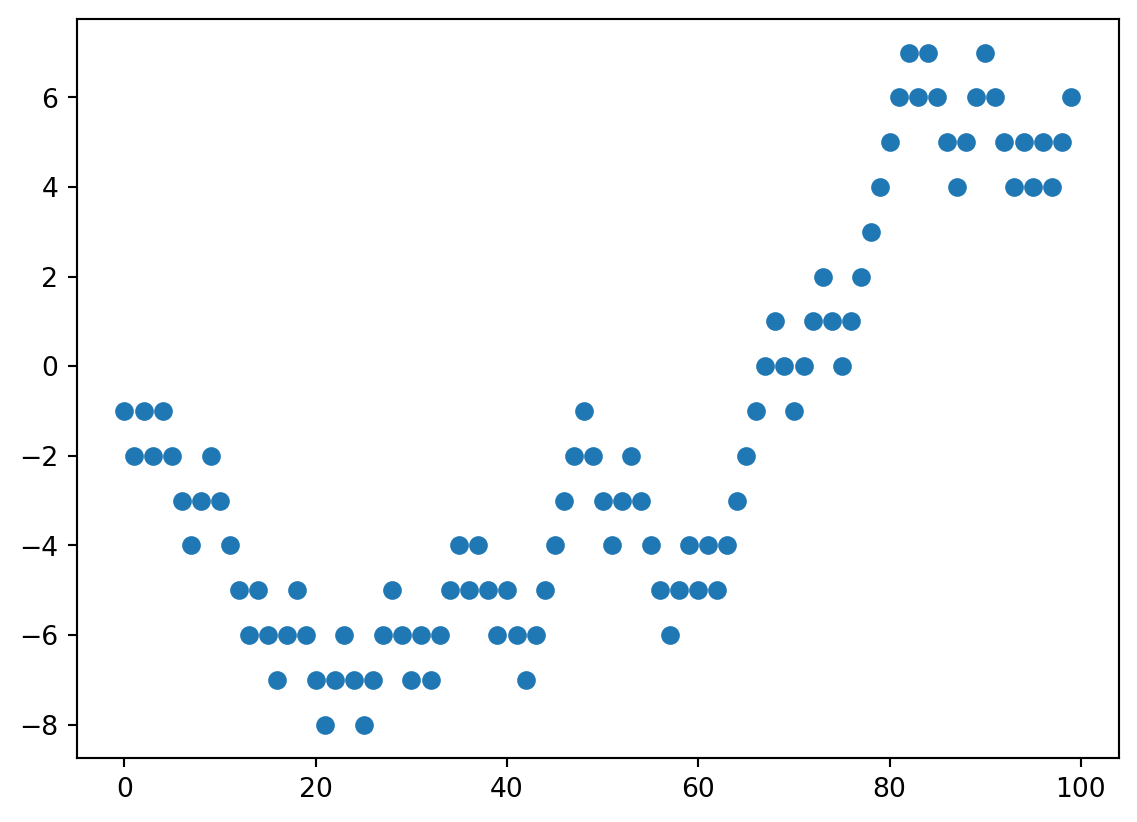
Por la definición de Equation 1 podemos estudiar la esperanza y la varianza de un conjunto de caminatas

In [6]:

t = arange(100)
vm = caminatas.mean(axis=1)
ds = caminatas.var(axis=1)

scatter(t,vm)

Figure 1: Valor medio o esperanza del conjunto de caminatas aleatorias a tiempo \(i\)

In [7]:

scatter(t,ds)

Figure 2: Varianza de las caminatas aleatorias

Se puede observar en Figure 1 la mayoria de las caminatas rondan el origen, y en Figure 2 como la varianza crece de manera lineal.

Cualquer duda consultar (Knuth 1984).

Knuth, Donald E. 1984. “Literate Programming.” Comput. J. 27 (2): 97–111. https://doi.org/10.1093/comjnl/27.2.97.